En ingenieria es común encontrar funciones que corresponden a estados de sí o no, o bien activo o inactivo. Por ejemplo, una fuerza externa que actúa sobre un sistema mecánico o una tensión eléctrica aplicada a un circuito , puede tener que suspenderse después de cierto tiempo. Para tratar de forma efectiva con estas funciones discontinuas conviene introducir una funcion especial llamada función escalón unitario.
Función de Heaviside.
3.5.1 Transformada de Laplace de la funcion escalon unitario
La transformada de la función de Heaviside es
En el primer teorema de traslación nos permitío calcular la transformada de una función F(t) al ser multiplicada por una función exponencial , el segundo teorema de traslación nos permitirá calcular la trasformada de una función que es multiplicada por una función escalón.
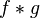 . (notar que el asterisco denota convolución en este contexto, y no multiplicación; a veces es utilizado también el símbolo
. (notar que el asterisco denota convolución en este contexto, y no multiplicación; a veces es utilizado también el símbolo  ). Sea
). Sea  el operador de la transformada de Fourier, con lo que
el operador de la transformada de Fourier, con lo que ![\mathcal{F}[f]](http://upload.wikimedia.org/math/7/4/d/74d8d9cf1fef828b858860c72324814c.png) y
y ![\mathcal{F}[g]](http://upload.wikimedia.org/math/2/7/2/272a59e139a86ba0444a744b4a29b4ca.png) son las transformadas de Fourier de f y g, respectivamente.
son las transformadas de Fourier de f y g, respectivamente. , podemos escribir:
, podemos escribir:![\mathcal{F}[f*g]=\sqrt{2\pi} (\mathcal{F}[f]) \cdot (\mathcal{F}[g])](http://upload.wikimedia.org/math/1/0/6/106196a2ef32816b06fb93fe11c6a3ad.png)
![\mathcal{F}[f \cdot g]=\frac{\mathcal{F}[f]*\mathcal{F}[g]}{\sqrt{2\pi}}](http://upload.wikimedia.org/math/3/b/4/3b406ce60d7a68eb656614f18460a00b.png)
![f*g=\sqrt{2\pi} \mathcal{F}^{-1}[\mathcal{F}[f]\cdot\mathcal{F}[g]]](http://upload.wikimedia.org/math/2/3/1/23184ac1f578fcd817a2e16b8cf98548.png)



